Mobile track #1 – EzDroid

Provided is an Android app package EzDroid.apk.

I typically use an Android emulator for testing, it’s free and easy to install on all major platforms, so it’s pretty much a no brainer.

After installation, it looks like it maanges to start but exits shortly after, for some unknown reason. Looks like it is time to inspect the code.

I like looking at high-level languages, so let’s start with that first.

My preferred method is to use dex2jar for decompilation, then using JD-GUI to explore the produced JAR file. You should have something that looks like the following screen:

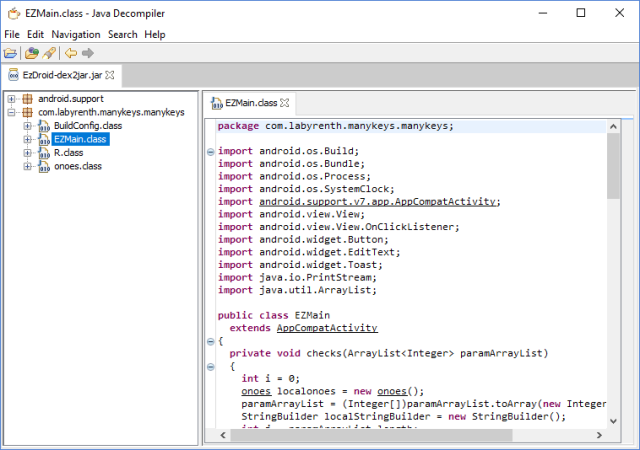
There’s only 2 packages, one of which is the Support Library, so the package with app code is likely com.labyrenth.manykeys.manykeys, with 4 classes inside:

• BuildConfig
• EZMain
• R
• onoes

BuildConfig and R are compile-time Android-generated classes, so ignore those.

EZMain looks to be the main Activity class. If you are unfamiliar with Android, that’s where the action happens.

Starting at the onCreate method of the Activity, there seems to be some checks:

public void onCreate(final Bundle paramBundle) {
  super.onCreate(paramBundle);
  setContentView(2130968602);

  paramBundle = new onoes();
  if (paramBundle.checkers(this).booleanValue() == true) {
    Toast.makeText(this, "You chose poor execution tactics...", 0).show();
    paramBundle.buh();
  }
  ...

onoes.checkers is what checks for the presence of the Android emulator. When we see the code for onoes.buh(), we now understand why the app never starts:

public void buh() {
  Process.killProcess(Process.myPid());
}

For the app to proceed, we need to patch away these killProcess calls; there’s more than one of them.

But actually, the app is very straightforward to analyze statically, so we can read the code and reconstruct its behaviour without needing to run it any further. Even if we had to, we can copy and paste the decompiled code into a Java file and run it locally, since it doesn’t depend on any special Android code.

There’s actually 3 parts to this challenge.

Part 1 & 2

The first part is gotten from onoes.retIt. You can copy and paste the retIt code into a Java file and run it to get the first part String:

Part1: PAN{ez_droid_

Part 2 is formed using what you see when you actually manage to run the app.

There’s a set of 12 numbers, each of which is prompted to you as EditText hints:

localObject = new String[12];
localObject[0] = "two plus one";
localObject[1] = "one plus one";
localObject[2] = "five plus two";
localObject[3] = "three plus zero";
localObject[4] = "nine minus two";
localObject[5] = "two plus two";
localObject[6] = "three plus three";
localObject[7] = "eleven minus ten";
localObject[8] = "negative two plus nine";
localObject[9] = "one plus one";
localObject[10] = "five plus two";
localObject[11] = "three plus one";

The onClick handler registered to the button contains the following logic, litered with emulator checks and killProcess calls with some SystemClock.sleep() to delay you.

The actual code it is supposed to reach is on the last line:

public void onClick(View paramAnonymousView)
{
  int j = Integer.parseInt(localEditText.getText().toString().trim());
  localArrayList.add(Integer.valueOf(j));
  if (this.i != 12)
  {
    localEditText.setHint(localObject[this.i]);
    localEditText.setText("");
    this.i += 1;
    return;
  }

  /* emulator detections ...
     more Process.killProcess() 
    and SystemClock.sleep() calls 
    here */

  EZMain.this.checks(localArrayList);
}

If you look at the checks code, it builds up the answers to the questions and calls onoes.hexToASCII:

while (i < j)
{
  localStringBuilder.append(paramArrayList[i].intValue());
  i += 1;
}
paramArrayList = localonoes.hexToASCII(localStringBuilder.toString());
System.out.println("Part 2: " + paramArrayList + "_");

We can do the same thing using Python, but we need the answers to those questions:

localObject[0] = "two plus one";  // --> 3
localObject[1] = "one plus one";  // --> 2
localObject[2] = "five plus two"; // --> 7
...

Once you have all 12 answers, we can use Python:

from binascii import unhexlify
print 'Part 2: ' + unhexlify('327374617274') + '_'

You will get “Part 2: 2start_“.

Part 3

Now the final part, which is also the hardest (especially if placed in a level 1 challenge),

  .
  .
  System.out.println("One last check...");
  if (localonoes.lastCheck("72657031616365746831732121").booleanValue() == true)
  {
    System.out.println("You did it, put the key together...");
    return;
  }
}

public Boolean lastCheck(String s) {
  if (Long.parseLong(s) * -37L + 42L == 17206538691L) {
    getHexString(s);
    System.out.println("\nDid you get it?  You should know...");
  }
}

It seems like we need lastCheck to return true, and in order to do that, the Long number passed in needs to satisfy the equation x * -37 + 42 = 17206538691.

As a hint, print unhexlify('72657031616365746831732121') gives you “rep1aceth1s!!“, so that needs to be replaced with a magic number.

While it does look like a simple math problem, it’s actually not.

x * -37 + 42 = 17206538691
x * -37 = 17206538649
x = 17206538649 / -37

The answer you get cannot satisfy the equation because this isn’t exactly regular arithmetic.

As a side note, someone even tried to get help by posting it on StackOverflow when the CTF started.

Computer Arithmetic

In Java, Long values are actually 64 bit numbers. If an arithmetic operation causes the number to be larger than 2⁶⁴, the upper bits of the number are simply truncated and the result wraps around.

When doing subtraction, there’s a magic representation for negative numbers called two’s complement. This representation behaves like a additive inverse, so all you need to do is to add numbers, no subtraction is necessary.

Similarly, there’s a magic representation that you can multiply to perform division. This is known as a multiplicative inverse. Such an inverse is defined for modular arithmetic, which is how we can model the wrap around behaviour of computer arithmetic (mod 2⁶⁴). Note that unlike two’s complement, not all numbers have a multiplicative inverse.

There’s a formula that can be used to find this inverse, called the extended Euclidean algorithm. If you want to see a worked example, refer to this Math Stack Exchange question.

We’ll use Go (or Golang) to solve this one, so it is as simple as calling a few functions:

a := uint64(17206538649) // 91 - 42 = 49
b := int64(-37)
bb := uint64(b) // re-interpret b as an unsigned 64-bit number

// modulus is 64 because Longs are 64-bits
big1 := bigInt(1)
N := new(big.Int).Lsh(big1, 64) // modulus is 1 << 64

invB := new(big.Int)
gcd := new(big.Int).GCD(invB, nil, bigInt(bb), N)

if gcd.Cmp(big1) != 0 {
    panic("GCD != 1")
}

The big.Int.GCD function is an implementation of the extended Euclidean algorithm, so it gets both GCD and our inverse in one operation.

In order for a multiplicative inverse to be defined, the GCD must be 1, i.e. N and the divisor (-37 in this case) must be co-prime.

Now that we have a number that represents “divide -37”, we should multiply this by 17206538649 to do the “division”:

x := new(big.Int).Mul(invB, bigInt(a))

// truncate to 64-bits
Nmask := new(big.Int).Sub(N, big1) // mask is 0xFFF... (64 bits)
x.And(x, Nmask)

fmt.Printf("ans = %d", x)

If we run the code, we get

ans = 12464016265554925723

But wait. There’s yet another catch. Long.parseLong would throw an Exception if you used this number.

Java numbers are always signed, so your number space gets split into half — positive and negative. Just as a signed char can store only from -128 to 127, as opposed to the full 0 to 255. This positive number is too large to fit into a signed Long, so we need to interpret it as a signed number:

fmt.Printf("ans = %d", int64(x.Uint64()))

And with that, we get

ans = -5982727808154625893

The full Golang code can be found in this gist. You can try out the code online at the Go Playground without having to install anything.

Z3

Alternatively, you can use my favourite method — the Z3 SMT solver. Z3 has BitVectors to simulate computer arithmetic. In a few lines of Python, we can solve the equation without knowing any math at all!

Basically you just need to define a variable x and the equation that it must satisfy and voilà:

from z3 import *

L = lambda n: BitVecVal(n, 64)

s = Solver()

x = BitVec('x', 64)
s.add(x * L(-37) + L(42) == L(17206538691) )

print s.check()

model = s.model()
print model
print model[x].as_signed_long()

Again, you still need to coerce Z3 to give you a signed number, thus providing you with the following output:

sat
[x = 12464016265554925723]
-5982727808154625893

Extremely effortless.

Once you give the right value to lastCheck, you should finally see.

Final Part: hard2defeat}

Piecing everything together thus gives you PAN{ez_droid_2start_hard2defeat}.